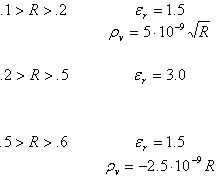
ECE 220 – Project
Bryan Berns & Peter Ognenoff
Problem Summary & Criteria Selection
SGFrameWork: MATLAB Coding & Graphical Explanation
Analytical Field Derivation: Electric Displacement
Analytical Field Derivation: Electric Field & Voltage
MATLAB Coding & Graphical Output of Analytical D-Field
If any code entry appears abnormally, expand your browser page to fit the entire screen.
Problem Summary & Criteria Selection
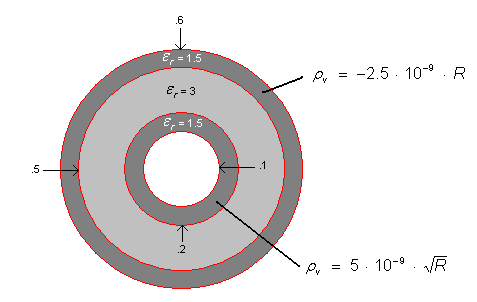
We will attempt to analyze the fields experience from a sphere with three dialectic spherical shells. The inner and outer shells posses a charge density that varies with radius. A cross-section of the sphere is shown below.
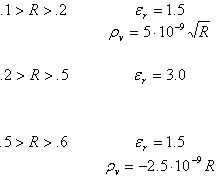

| CONST NMAX = 5000;
// SETUP FOR 5000 POINT ITERATION CONST DR = 0.0002; // FROM R = 0 TO R = 1. CONST PI = 3.1415927; CONST EPS0 = 8.8542E-12; VAR E[NMAX], D[NMAX], V[NMAX], RHO[NMAX], R[NMAX], A[NMAX], EPSR[NMAX]; BEGIN MAIN ASSIGN R[I=ALL] = I*DR; // ARRAY OF RADIUS VALUES ASSIGN RHO[I=500..1000] = sqrt(R[I])*5.0E-9; // SOLVE CHARGE FOR FIRST SHELL ASSIGN RHO[I=2500..3000] = R[I]*-2.5E-9; // SOLVE CHARGE FOR SECOND SHELL ASSIGN A[I=ALL] = 4*PI*sq(R[I]); // ARRAY OF VARYING SURFACE AREA ASSIGN EPSR[I=ALL]=1.0; // DEFAULT PERMITTIVITY CONSTANT ASSIGN EPSR[I=500..1000]=1.5; // PERMITTIVITY FOR FIRST DIALECTIC SHELL ASSIGN EPSR[I=1000..2500]=3; // PERMITTIVITY FOR SECOND DIALECTIC SHELL ASSIGN EPSR[I=2500..3000]=1.5; // PERMITTIVITY FOR THIRD DIALECTIC SHELL ASSIGN D[I=1..NMAX-1] = (A[I-1]*D[I-1]+RHO[I]*A[I]*DR)/A[I]; // FLUX(IN) + FLUX(OUT) / AREA ASSIGN E[I=ALL] = D[I]/(EPS0*EPSR[I]); // D-FIELD / EPSILON ASSIGN V[I=1..NMAX-1] = V[I-1]-E[I]*DR; // V(PREVIOUS) – E*RADIUS ASSIGN V[I=ALL] = V[I]-V[NMAX-1]; / ADJUST SO V(MAX)=0 WRITE; END |
SGFrameWork: MATLAB Graphical Output
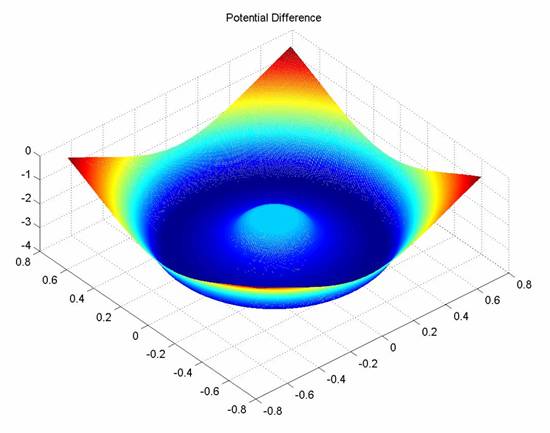
SGFrameWork: MATLAB Coding & Graphical Explanation
First Graphs
|
clear
all;
%clear all current variables
load V.000; load D.000; load
R.000;
R = [-b:b]; %and create a vector of those values
|
Second Graphs
| clear all %clear all current
variables close all %close all current graphs load V.000 |
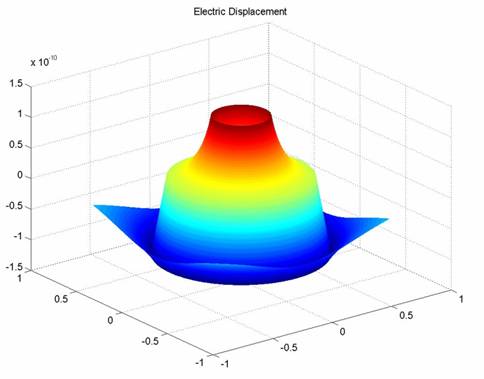
Electric Displacement:
Since there is no charge from 0 to .1, there is no D-Field.
When the radius reaches .1 the D-Field increases because of the positive charge density.
When the radius reaches .2, the D-Field begins to drop as the charge moves farther away.
When the radius reaches .5, the D-Field begins to drop suddenly due the presence of a negative charge density.
As the radius beyond .6, the field weakens and tapers toward zero as all charges move farther away.
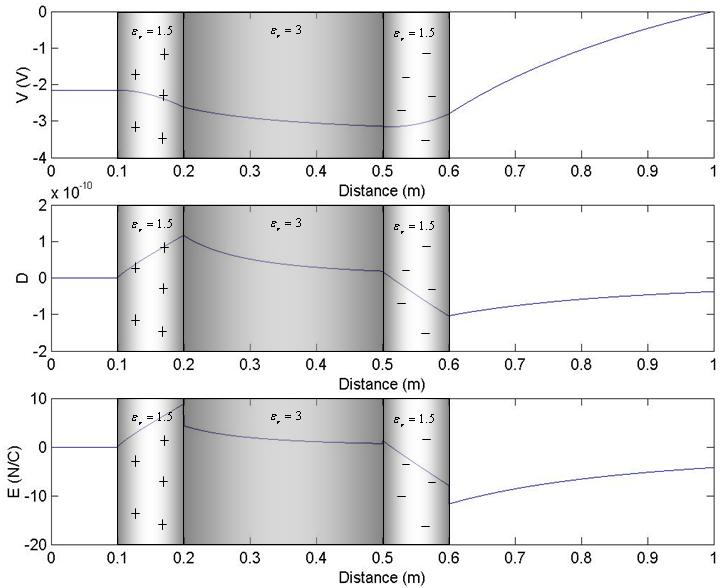
Electric Field:
The the E-field is proportional to the D-Field with bias to the different epsilons it experiences.
At the boundary of .2, we see the E-Field decrease to one-half its magnitude due to the ratio of permittivities -- 3.0:1.5
At the boundary of .5, we see the field double (although it's not easy to view on the displayed graph). Same reason but reciprocal ratios -- 1.5:3.0
At the boundary of .6, the E-field's magnitude again changes due to the permittivity ratios: 1:1.5
Analytical Field Derivation: Electric Displacement

Analytical Field Derivation: Electric Field & Voltage
We choose not to evaluate the Voltage integrals seeing as the complexity of our equations was increasing.

MATLAB Coding & Graphical Output of Analytical D-Field
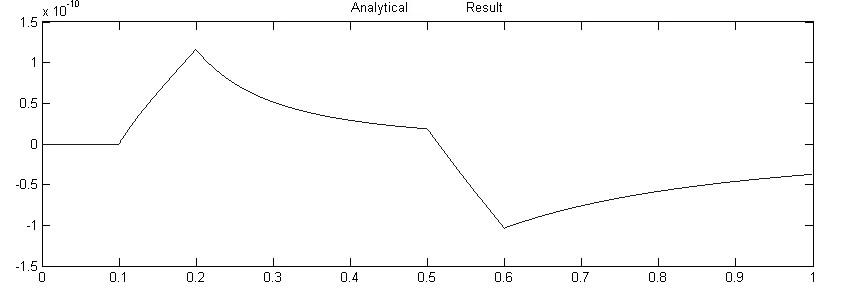
The below graph is generated from using the derived D-Field equations. It matches the SGFrameWork output to with very little error.
MATLAB Code
| clear all %clear all current
variables close all %close all current graphs load R.000 s = size(R,1); % FOR .1 < R < .2 D(0.1*s:0.2*s) = (10^-8)*( R(0.1*s:0.2*s).^3.5-0.1^3.5)./(7*R(0.1*s:0.2*s).^2); % FOR .2 < R < .5 D(0.2*s:0.5*s) = (10^-8)*(0.2^3.5-0.1^3.5)./(7*R(0.2*s:0.5*s).^2); % FOR .5 < R < .6 D(0.5*s:0.6*s) = (10^-8)*(0.2^3.5-0.1^3.5)./(7*R(0.5*s:0.6*s).^2) + (-2.5*10^-9)*(R(0.5*s:0.6*s).^4-.5^4)./(4*R(0.5*s:0.6*s).^2); % FOR .6 < R D(0.6*s:1.0*s) = (10^-8)*(0.2^3.5-0.1^3.5)./(7*R(0.6*s:1.0*s).^2) + (-2.5*10^-9)*(0.6^4-0.5^4)./(4*R(0.6*s:1.0*s).^2); plot(R,D); title('Analytical Result'); |
The only real problems we encountered during this project, other than trying to find an 'interesting' field setup, was related to precision. The 100 point evaluation used initially in the SGFrameWork setup was not evaluating the fields to the precision we desired. As the fields developed, these precisions errors were causing our calculator results to be disturbingly different. The solution was to use more points, so we adapted the SGFrameWork simulation to use 5000 points. After that, everything was happy.